数学建模

数学建模
chfychin🥝数学建模:应用定量的思维方式探讨自然现象、社会现象解决实际问题。
建模步骤:
当模型为非曲线时,可以将其化为直线:
- 1.图象向下凸可以将横坐标的次方系数适量增大,反之,横坐标次方系数减小。(次方系数可出现分数)
- 2.当开头结尾都受限制时,可以考虑他的增长率
二、动力系统
线性动力系统:
- 1.令$a_{n+1}=r*a_n$,则它的解为$a_n=r^na_0$,其中$a_0$为给定初始值。
- 2.当 $a0=a$时,如果对所有的n=1,2,3,…有则将数α称为动力系统 $a{n+1} =f(a_n)$的平衡点或不动点。即 $a_n=a$是该动力系统的常数解。
- 3.线性动力系统解的长期趋势:
| r | 趋势 | ||
|---|---|---|---|
| r=0 | 常数解以及在0处的平衡点 | ||
| r=1 | 所有初值都是常数解 | ||
| r<0 | 震荡 | ||
| $\ | r\ | $<1 | 衰减到极限值为0 |
| $\ | r\ | $>1 | 无限增长 |
形如 $a_{n+1}=ra_n+b$ 的动力系统
- $a_{n+1}=ra_n+b$,其平衡点是$a=\frac{b}{1-r},r\neq1$
- 当$r=1,b=0$时,每个初始值都是平衡点
- 当$r=1,b!=0$时,不存在平衡点。
形如 $a_{n+1}=ra_n+b,(r\neq1)$ 的动力系统
- 解为:$a_n=r^nc+\frac{b}{1-r}$,(c是依赖初始值的某一常数)
- 对于动力系统$a_{n+1}=ra_n+b,(b\neq0)$
| r的值 | 长期趋势 |
| ———— | ———— |
||r|<1|稳定平衡点| |\|r\|>1|不稳定平衡点|
|r=1|没有平衡点|三、建模过程
模型准备—>模型假设—>模型建立—>模型求解—>模型分析—>模型检验—>模型应用四、模型拟合准则:
按照一个或一些选出的模型类型对数据进行拟合。切比雪夫准则
切比雪夫准则对有大偏差的单个数据点赋以更大的权重,当极小化最大绝对偏差很重要时可以采用这一准则。 - 给定某一函数类型$y=f(x)$及m个数据点$(xi,y_i),j=1,2,3,···,m$.该切比雪夫准则是在整个数据点集上使最大绝对值偏差:$min{\max{1 \leq i \leq m}|y_i-f(x_i)|}$最小.
极小化绝对偏差之和
- 给定某一函数类型$y=f(x)$及m个数据点$(xi,y_i),j=1,2,3,···,m$.确定函数类型$y=f(x)$的参数,使绝对值偏差之和:$min{\sum{i=1}^{m}|y_i-f(x_i)|}$最小
- 极小化绝对偏差之和这个准则赋以每个数据点相同的权重,其稳健性较好,对异常值不太敏感,常用数值解法求出近似解。。
最小二成准则
- 给定某一函数类型$y=f(x)$(参数待定)及m个数据点$(xi,y_i),j=1,2,3,···,m$.该准则是确定函数类型$y=f(x)$的参数,使偏差平方和:$min{\sum{i=1}^{m}({y_i-f(x_i)})^2}$最小
- 最小二乘准则对偏差较大的数据点赋以较大的权重对偏差较小的数据点赋以较小的权重,其稳健性较差对异常值敏感。
与前两个准则相比,最小二乘准则产生的优化问题易于解析求解。由于偏差平方和是一个连续函数,可对待定参数求偏导得到正规方程,通过正规方程来确定最优参数进而确定出所给函数类型中的最佳函数。
回归分析
回归分析
由来
由来:英国著名统计学家高尔顿是最先应用统计方法研究两个变量之间关系问题的人。高尔顿研究发现父母身高与儿女身高之间有这么一种关系:父母高->儿女也高,父母矮->儿女也矮
| 父母平均身高 | 儿女平均身高 |
|---|---|
| 高一个单位 | 高半个单位 |
| 矮一个单位 | 矮半个单位 |
逐步回归
具有回归于人口总平均高的趋势
用高尔顿的话说,儿女身高“回归”到中等身高。这就是回归一词的最初由来。把这种后代的身高向中间靠拢的趋势称为“回归现象”。
后来,人们把由一个变量的变化去推测另一个变量的方法称为为“回归方法”。
为何使用回归分析
(1) 更好地了解:
对某一现象建模,以更好地了解该现象并有可能基于对该现象的了解来影响政策的制定以及决定采取何种相应措施。基本目标是测量一个或多个变量的变化对另一变量变化的影响程度。示例:了解某些特定濒危鸟类的主要栖息地特征(例如:降水、食物源、植被、、天敌),以协助通过立法来保护该物种。
(2) 建模预测:
示例:如果已知人口增长情况和典型的天气状况,那么明年的用电量将会是多少?
(3) 探索检验假设:
还可以使用回归分析来深入探索某些假设情况。假设您正在对住宅区的犯罪活动进行建模,以更好地了解犯罪活动并希望实施可能阻止犯罪活动的策略。开始分析时,您很可能有很多问题或想要检验的假设情况。
回归分析的作用主要有以下几点
- 挑选与因变量相关的自变量;
- 描述因变量与自变量之间的关系强度;
- 生成模型,通过自变量来预测因变量:
- 根据模型,通过因变量,来控制自变量。
是一种预测预报方法,提前知道未来的状态和发展趋势。
它研究的是因变量Y和自变量X之间的关系,是一种预测性的建模技术。
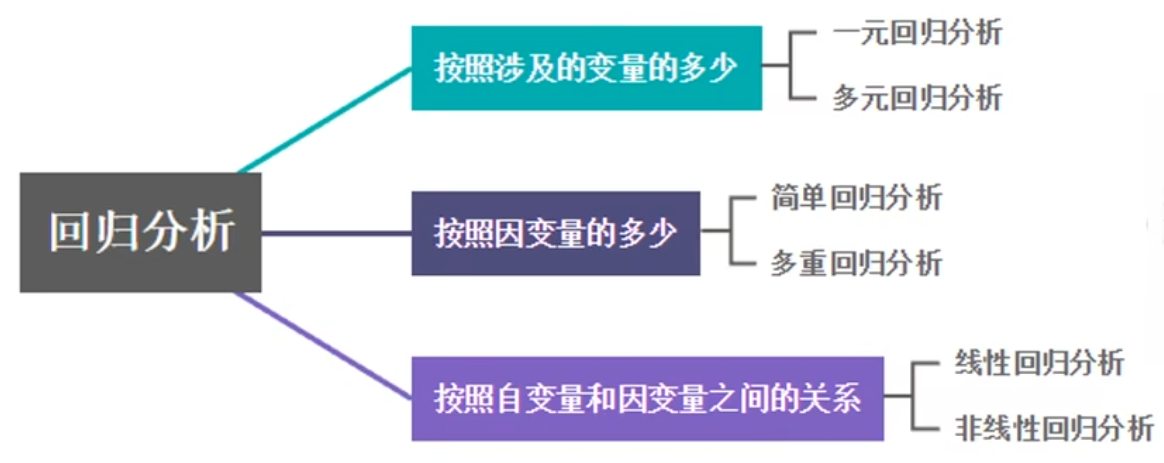
线性回归
| 线性 | 非线性 |
|---|---|
| 一元线性回归 | 一元非线性回归 |
| 多元线性回归 | 多元非线性回归 |
一元线性回归
一元线性回归可用来分析自变量x取值与因变量y取值的内在联系,这里的自变量x是确定性的变量,因变量y是随机性的变量。
一元线性回归模型构建
一元线性回归的模型为: $y=a+bx+ε目ε\sim N(0,σ^2)$
- 其中$a$表示截距,$b$表示直线的倾斜率;$a、b$称为回归系数,与自变量$x$无关。
- $ε$ 是随机误差项,并总是假设$ε\sim N(0,σ^2)$。
若对自变量x与因变量y分别进行n次独立观测,得到:
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| $X$ | $x_1$ | $x_2$ | ··· | $x_n$ |
| $Y$ | $y_1$ | $y_2$ | ··· | $y_n$ |
对于参数a,b用最小二乘法估计,即应选取估计值,6,使当$a=\hat{a},b=\hat{b}$ 时$\hat{yi}$与估计值$\hat{y_i}=\hat{a}+\hat{b}x$, 误差平方和 $Q=\sum{i=1}^n{εi}^2=\sum{i=1}^n{(y_i-\hat{y_i})}^2$达到最小。
为此,我们令
- $\frac{\partial Q}{\partial a}=-2\sum_{i=1}^n{(y_i-a-bx_i)}^2=0$
- $\frac{\partial Q}{\partial b}=-2\sum_{i=1}^nx_i{(y_i-a-bx_i)}^2=0$
得
- $\hat{b}=\frac{\sum{i=1}^n(x_i-\overline{x})(y_i-\overline{y})}{\sum{i=1}^n{(x_i-\overline{x})}^2}$
- $\hat{a}=\hat{y_i}-\hat{b}\overline{x}$
$\hat{a},\hat{b}$为$a,b$的最小二乘估计,其中分别是$\overline{x},\overline{y}$分别是 x,y, 的样本均值。
回归方程的检验
回归方程的假设检验:
- 回归模型的假设检验
- 回归系数的假设检验
回归模型的假设检验
检验原因:因变量y与自变量x之间是否存在如模型所表示的关系是需要检验的。
方法:F检验法
- 模型的误差平方和为: $SSE=\sum_{i=1}^n{(y_i-\hat{y_i})}^2$
- 模型的回归平方和为: $SSR=\sum_{i=1}^n{(\hat{y_i}-\overline{y_i})}^2$
- 模型的总离差平方和为: $SST=\sum_{i=1}^n{(y_i-\overline{y_i})}^2$
- 可得: $SST=SSE+SSR$
对于模型$y=a+b_ix_i+ε,i=1,2…,p.$
显然,模型成立的对立面是: y与x的线性关系不明显,即$b_i$很小,所以我们可以令原假设为$H_0:b_1=b_2=…=b_p=0$,如果原假设成立,则构造统计量
p是自变量个数,$\hat{σ}^2=MSE=SSE/(n-p-1)$ 是 $σ^2$ 的无偏估计。
在显著性水平$\alpha$下,对于上$\alpha$分位数 $F\alpha(p,n-p-1)$,若 $F<F\alpha(p,n-p-1)$,则接受$H_0$,否则拒绝$H_0$。
注:这里接受H。只是说明了y与x的线性关系不明显,也可能是非线性关系,如平方关系
另一种方法:通过判定系数来衡量$y$与$x_1,x_2,…,x_n$,的相关程度。即(回归平方和在总平方和中的比值):
其中,$R=\sqrt{R^2}$ 称为复相关系数,$R$ 越大(通常大于$0.8$或$0.9$),$y$与$x_1,x_2,…,x_n$的相关关系越密切。
回归系数的假设检验
检验原因: 当前面的回归模型检验通过,对自变量系数的检验,即考察每一个自变量对因变量的影响是否显著。
方法: $t$ 检验法(做 $p+1$ 次检验)
$\quad$设随机变量$x1,x_2,…,x_n$对应的系数为 $\hat{b_1},\hat{b_2},…,\hat{b_n}$,各个 $x_i$ 都服从正态分布, 所以 6也服从正态分布。($b_0=a$)
当 $H_0: b_i=0,i=0,1,2..p.$ 成立时,有$$
t_i=\frac{b_j/ \sqrt{c{ii}}}{\sqrt{SSE/(n-p-1)}}\sim t
(n-p-1)$$
($c_{ii}$:是正规方程组的系数矩阵的逆矩阵中的元素)
在显著性水平$\alpha$下,若$ti<t{\frac{\alpha}{2}}(n-m-1)$,则接受$H_0$, 否则拒绝$H_0$: 认为系数不为0.即通过检验。
利用回归模型进行预测(点预测和区间预测)
$eg$: 总体数量为 $n$,对总体的均值进行预测。
(1)当 $x=x_0$ 时,用方程立 $\hat{y_0}=a+bx_0$。预测 $y_0$ 的值,为点预测。($\hat{y_0}$)
(2)当 $x=x_0$,时,用区间去换测 $y$ 的取值范围,为区间预测。([$\hat{y_0}-\Delta{x},\hat{y_0}+\Delta{x}$])
一元非线性回归
一元非线性回归介绍
$\quad$ 非线性回归是回归函数关于未知回归系数具有非线性结构的回归。简单理解就是非线性回归就是曲线回归。
$\quad$ 实际问题中,变量之间常常不是直线。这时,通常是选配一条比较接近的曲线,通过变量替换把非线性方程加以线性化,然后按照线性回归的方法进行拟合。(将非线性转化为线性)。
$\quad$ 在做非线性回回归时,一般要先确定该非线性回归模型后再做非线性回归;
$\quad$ 解题思路是先将所给的数据点通过matlab绘图的方式画出来,再看看画出来的散点图比较符合哪个非线性回归模型就选择那个模型,最后再做非线性回归分析。
转化为一元线性常用 取对数再做回归
如:我们可以通过对因变量或者自变量进行一定的变形,将问题转化为一元线
性回归分析。
|曲线回归方程|方法|转换后的直线回归方程|
|:-:|:-:|:-:|
|$y=a+\frac{b}{x}$|对自变量x取倒数|$y=a+bx’$|
|$y=ax^b$|将方程两边取对数|$lny=lna+blnx$|
|$y=ae^{bx}$|将方程两边取对数|lny=lna+bx|
| 曲线回归方程 | $y’$ | $x’$ | $a’$ | $b’$ | 转换后的直线回归方程 |
|---|---|---|---|---|---|
| $\hat{y}=ae^{bx}(a>0)$ | $y’=lny$ | $a’=lna$ | $y’=a’+bx$ | ||
| $\hat{y}=ab^x(a>0)$ | $y’=lny$ | $a’=lna$ | $b’=lnb$ | $y’=a’+b’x$ | |
| $\hat{y}=a+blnx(x>0)$ | $y’=lny$ | $x’=lnx$ | $y’=a+bx’$ | ||
| $\hat{y}=ax^b(a>0,x>0)$ | $y’=lny$ | $x’=lnx$ | $a’=lna$ | $y’=a’+bx’$ | |
| $\hat{y}=\frac{x}{a+bx}(x\neq-\frac{a}{b})$ | $y’=\frac{x}{y}$ | $y’=a+bx$ | |||
| $\hat{y}=\frac{a+bx}{x}(x\neq0)$ | $y’=yx$ | $y’=a+bx$ | |||
| $\hat{y}=\frac{1}{a+bx}(x\neq-\frac{a}{b})$ | $y’=\frac{1}{y}$ | $y’=a+bx$ | |||
| $\hat{y}=\frac{k}{1+ae^{-bx}}(a>0)$ | $y’=ln(\frac{k-y}{y})$ | $a’=lna$ | $y’=a’-bx$ |
步骤
1.描散点图,确立回归方程的模型;
2.求方程中待定系数,建立回归方程:
- 将非线性方程化为线性方程;
- 求待定系数,建立线性方程;
- 对线性方程作回归关系显著性检验;
- 将线性方程还原为非线性。
多元线性回归
多元线性回归介绍
$\quad$ 在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。实际应用中,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。总的来说,回归分析就是用来做预测的,多元回归要比一元回归更加高效实用。
$\quad$ 多元回归分析是研究多个变量之间的关系的回归分析方法,是反映一种现象或事物的数量依多种现象或事物的数量的变动而相应地变动的规律,建立多个变量之间线性或非线性数学模型数量关系式的统计方法。
多元线性回归模型
多元线性回归模型通常用来描述变量$y$和$x$之间的随机线性关系,即:
- $y=\beta_0+\beta_1x_1+…+\beta_mx_m+\varepsilon$
- $ε$ 是随机误差项,并总是假设$ε\sim N(0,σ^2)$。
式中: $\beta_0,\beta_1,…,\beta_m,σ2$ 都是与 $x_1,x_2,…,x_m$ 无关的未知参数,其中 $\beta_0,\beta_1,…,\beta_m$ 称为回归系数。
多元非线性回归
多元非线性回归介绍
$\quad$ 建立多元非线性回归方程在科学研究中应用广泛,其重要方法是将非线性回归方程转化为线性回归方程。
转化时应首先选择合适的非线性回归形式,并将其线性化,确定线性化回归方程的系数,最后确定非线性回归方程中的参数。
$\quad$ 首先决定非线性模型的函数类型,对于其中可线性化问题则通过变量变换将其线性化,从而归结为前面的多元线性回归问题来解决。
$\quad$ 选择合适的曲线类型不是一件轻而易举的工作,首先对原始数据作图或则依靠专业知识和经验,来选择适当的函数进行拟合。
常用的曲线类型有幂函数,指数函数,抛物线函数,对数函数和S型函数
回归分析中的:线性&非线性
线性函数 $\neq$ 线性回归方程
$Yi=\beta_0+\beta_1x{i1}+…+\betapx{ip}+\varepsilon_i$
$Y_i=\beta_1x_1+\beta_2x_i^2+\varepsilon_i$
$Y=\beta_0+e^\beta_1x_1+\varepsilon$
方程一和方程二为线性回归,方程三为非线性回归。
线性回归中线性的含义: 因变量$y$对于未知的回归系数($\beta_0,\beta_1,…,\beta_k$)是线性的。这就是问题中所说的参数线性。换句话说只要系数B是线性的就称为线性回归,方程一和方程二中的回归系数B都是线性的,而方程三中自变量X1的回归系数为非线性,因此,方程一和方程二为线性回归,方程三为非线。